-expressions
may all be referred to as operators, despite the
obvious differences in their semantics. An evaluable expression, the
CAR of which is an operator, will be referred to as that
operator's form.
This paper appears in the
Conference Record of the 1980 Lisp Conference,
Stanford University, August 25-27, 1980.
The substance of the original text appears in normal fonting,
though a small number of out-and-out typos were corrected.
Oddities of spelling that were the custom of the time
(either generally, or just for me) were left alone.
Some formatting of headings and tables was adjusted slightly for HTML.
Any new text that has been added appears
bracketed and in color green; such text is intended to
help clarify the historical context, since considerable time
passed between the time this paper was published and the time I
converted it to HTML.
--Kent Pitman, 11-Oct-1998.
Annotated original document follows.
Click here for an index
of other titles by Kent Pitman.
Kent Pitman
[address at time of publication]
MIT Laboratory for Computer Science
545 Technology Square
Cambridge, MA 02139
Special forms are those expressions in the Lisp language which do not follow normal rules for evaluation. Some such forms are necessary as primitives of the language, while others may be desirable in order to improve readability, control the evaluation environment, implement abstraction and modularity, affect the flow of control, allow extended scoping mechanisms, define functions which accept a variable number of arguments, or achieve greater efficiency. There exist several long-standing mechanisms for specifying the definition of special forms: FEXPR's, NLAMBDA's, and MACRO's.
In this paper, the motivations for using special forms are discussed, followed by a summary of the advantages and disadvantages of employing MACRO's, FEXPR's, and NLAMBDA's as tools for their implementation. It is asserted that MACRO's offer an adequate mechanism for specifying special form definitions and that FEXPR's do not. Evidence is given which supports the author's contention that FEXPR's interfere with the correct operation of code-analyzing programs such as the compiler. Finally, it is suggested that, in the design of future Lisp dialects, serious consideration be given to the proposition that FEXPR's should be omitted from the language altogether.
In the past decade [1970's], Lisp has evolved as the clear favorite among languages used by members of the AI community for implementing programs and systems. The sophistication of such systems, however, is not necessarily reflected in the code which holds them together. The underlying code may be a patchwork of very low-level constructs which when examined individually offer little information about the high-level problem they are attempting to solve.
Many modern programs [in 1980] are still written in terms of CAR, CDR and CONS rather than high-level primitives that insulate the main program from the representation of its data. The justifications may vary, but in many cases it just comes down to an ignorance of the options available. Some programmers may claim that use of the more sophisticated programming constructs of the language are unnecessary, and that use of these constructs introduces a level of complexity to the code which is unnecessary. Others may fear that their desire for efficiency must preclude any attempts at elegance of coding style.
Over the past two years [1978-1980], there has been a great increase in the expressive power of the Lisp dialects used in the MIT community [1]--owing to a large degree to the development of a large number of sophisticated general-purpose software packages which allow a programmer to quickly and efficiently bootstrap high-level data and program structures to use as ``primitives'' for programming at an even higher level. In the course of this development, a number of issues have been raised about what low level primitives should be used to implement these software packages.
In the course of this boom in software development, MACRO's have demonstrated their power as tools for the implementation of new systems. More importantly, it has become clear that such programming constructs as NLAMBDA's and FEXPR's are undesirable for reasons which extend beyond mere questions of aesthetics, for which they are forever under attack. Indeed, the presence of these constructs in the language make it impossible to develop general-purpose program-manipulation software (e.g., compilers and macro packages) which can function with any reasonable degree of reliability. There exists an inherent potential for error which means that certain programs, no matter how carefully conceived, must in the end function only heuristically. It is with these issues that this paper will attempt to deal.
Non-atomic, evaluable Lisp expressions may be divided into two fundamental classes: functional applications and special forms. Functional applications involve `normal' evaluation--arguments are evaluated from left to right in most dialects [2], followed by an application of a functional object to the result of the evaluations. Special forms involve any syntactic or semantic deviation from this description.
[Common Lisp (1984) later partitioned the same set of expressions into three groups, not two. In Common Lisp, ``macros'' are not ``special forms.'' But at the time of this paper, we were still calling ``macros'' a kind of ``special form''; and what Common Lisp calls ``special forms'' we were calling ``primitive special forms.'' Personally, I still prefer the older definition used in this paper.]
For simplicity, we shall use the term operator to mean the
functional description of how any Lisp form is to be evaluated. It
will be used as the generic term to refer to any object which may
legitimately appear in the CAR of an evaluable expression.
By this definition, CAR, COND, and
-expressions
may all be referred to as operators, despite the
obvious differences in their semantics. An evaluable expression, the
CAR of which is an operator, will be referred to as that
operator's form.
Before embarking on a discussion of how special forms are or should be implemented, we should first take a look at the various ways in which it may be desirable to use them in a real programming environment, in an attempt to identify the issues with which an implementation of special forms must attempt to deal.
In order to do symbolic programming there is a need for at least one special form which does no argument evaluation. For this purpose, Lisp has QUOTE. Having the ability to say (QUOTE (A B C)) to refer to a piece of structure rather than the result of evaluating that piece of structure is fundamental to many forms of Lisp programming.
In addition, a small number of special forms that make up primitive control structure are also useful (e.g., LAMBDA expressions to describe functions and COND to provide conditional branching).
These fundamentally important forms, out of which the rest of the language is constructed, will be called primitive special forms. They may be handled in special ways by the interpreter or compiler in order to accomplish their function.
There are situations in Lisp in which it is so rare that one would like the argument to a function to evaluate, that one might wish to define a function which inhibited the evaluation of its arguments rather than have to manually quote them every time the function was used.
[At the time this paper was written, the Lisp read-eval-print loop was the interface to Lisp. Computers didn't have `window systems' in the modern sense of the word, nor had the term GUI come into existence yet, nor was there even the notion of a command interface in Lisp separate from program interfaces. As such, we're really talking here about the `abuse' of linguistic terms, like TRACE and DESCRIBE, to accomodate what later came to be seen as user interface needs.]
For example, suppose we have a friendly system that offers a function named DESCRIBE, which can be called in order to have documentation on a function typed out on the console. That function might be defined as:
(DEFUN DESCRIBE (ITEM)
(PRINC (LOOKUP-DOCUMENTATION ITEM)))
and a typical call to the function might look like
(DESCRIBE 'CDR).
After repeated use a Lisp user is likely to tire of having to explicitly quote the argument. It may be that he never wants documentation on a topic which is the value of a variable or the result of evaluating an expression. He may find himself omitting the quote unconsciously and grumbling angrily when an error is generated trying to evaluate an unbound symbol. Why shouldn't he be able to have a function which had the syntax
(DESCRIBE CDR)
if that's the way he will always wish to type it in? Flexibility in syntax, if it does not lead to ambiguity, would seem a reasonable thing to ask of an interactive programming language.
In addition to having a language which was easy to work with interactively, a programmer might like the ability to lay out his program in a way that is visually comfortable for him to read or edit later on.
Let us suppose that we would like to compute the value of the expression
To avoid the expense of recomputing the
and
functions, we might wish to employ LAMBDA variables
to store the result of the calls. In primitive Lisp code, this would
look like
((LAMBDA (G P)
(+ (* (+ G P) G)
(* 3.14159265 P P)))
(GAMMA X)
(PSI X))
As the size of the LAMBDA's body increases, however, the formal and actual parameters are pushed father and farther apart due to the nature of this syntax. Hence we would like some way of laying things out so that they are easy to read and yet can be recognized by the evaluator as ``just another way of specifying a LAMBDA combination.'' The following syntax, for example, might express the same meaning as our previous LAMBDA combination:
(LET ((G (GAMMA X)) (P (PSI X)))
(+ (* (+ G P) G)
(* 3.14159265 P P)))
Another use of special forms arises in the case where we have a function and would like its arguments evaluated--but not immediately. We might first wish to create some sort of special environment for the evaluation.
Consider the case of a Lisp which supports arbitrary handlers for interrupts received from the terminal or the operating system. If an interrupt is received, the Lisp suspends any work currently executing and passes control to the handler. Upon return from the handler, the suspended computation is resumed from the point where it was executing prior to the interrupt. Given an environment in which code may be expected to be interrupted at any point, it may become necessary to protect certain pieces of critical code which if suspended at a wrong point would leave the environment in an inconsistent state.
Suppose that there exists some reserved variable named DEFER-INTERRUPTS which will be checked by the Lisp when an interrupt is received and, if bound to a non-null value, will cause the Lisp to queue that interrupt for processing at a later time when the scope of that binding has been popped. Almost invariably, we would want to bind this value to T, run some code, and then unbind it. It might be useful, therefore, to give the user a primitive with syntax such as
(WITHOUT-INTERRUPTS form1 form2 ...),
which would behave just like PROGN, except that the evaluation of the list of forms would be delayed long enough to establish an environment in which interrupt-handling would be inhibited. This is equivalent in practice to saying
((LAMBDA (DEFER-INTERRUPTS)
form1 form2 ...)
T)
but it is more than the mere cosmetic change: By using the WITHOUT-INTERRUPTS construct, the user has freed himself of the need to know how or where the interrupt-inhibiting flag is actually stored. It may be possible for him to obtain this information, but it is not necessary.
The examples we have seen with LET and WITHOUT-INTERRUPTS illustrate another motivation for the use of special forms: abstraction. It may be that we don't care that LET is implemented via a LAMBDA or that WITHOUT-INTERRUPTS is going to bind a magic variable. We can abstract out a higher purpose for the form, and as long as it accomplishes that high-level purpose, the details of its implementation can be left to vary as changes are introduced to the language or programming environment.
Special forms may also be desirable to affect flow of control. Lisp built-in operators such as PROG and COND fall into this category. Suppose we would like to allow new, user-defined control structures.
A simple example of this would be the creation of an IF special form which had the same effect as a simple COND. We might want the IF to have the syntax
(IF antecedent consequent alternative)
which would have the same meaning as
(COND (antecedent consequent)
(T alternative))
In this example, we can see that not only must one of the arguments (the antecedent) be evaluated before the other arguments, but one of the two other arguments will not be evaluated at all. Here a normal Lisp EXPR [3] description such as
(DEFUN IF (CONDITION T-VAL NIL-VAL)
(COND (CONDITION T-VAL)
(T NIL-VAL)))
is clearly wrong because the user may wish to write code which depends on being executed if and only if antecedent is true. Using the EXPR definition, code such as
(IF (ATOM X) X (CAR X))
which depends on (CAR X) not being evaluated if the value of X turns out to be an atom, would be unable to run.
One might propose, then, that the expression
(IF (ATOM X) 'X '(CAR X))
is what we want, since neither the consequent nor the alternative is executed in the original function call. A definition of this IF might look like
(DEFUN IF (CONDITION T-VAL NIL-VAL)
(COND (CONDITION (EVAL T-VAL))
(T (EVAL NIL-VAL))))
This is also inadequate, however, because of the scoping problem. Most Lisps [in 1980] are dynamically scoped--i.e., the scoping of variables is determined by the dynamic, or runtime, environment rather than by the lexically apparent environment in which they were defined. The following simple example should illustrate why this second alternative to the IF problem will not work:
(SETQ T-VAL 0 NIL-VAL 1)1 (IF T 'T-VAL 'NIL-VAL)
The symbol T-VAL is returned, rather than 0, because at the time of the call to EVAL, T-VAL has been locally bound.
[Users of the SCHEME language might assume that the solution of
(IF antecedent (LAMBDA () consequent) (LAMBDA () alternative))would immediately present itself. However, SCHEME was only 2 years old at the time and did not have a very big following yet. In fact, though SCHEME's idea of lexical scoping (which in turn derived from Algol's) was used a few years later in Common Lisp (1984), even lexical scoping was considered ``highly experimental'' by some in the Lisp community. Those of us who believed lexical scoping safe pretty much had to force it down some other people's throats. So don't let ``20/20 hindsight'' allow you to be confused into thinking that such a solution was obvious. And, in any case, even the SCHEME community doesn't think the solution to the ``IF problem'' is to have a function named IF that always takes closures as arguments. So the global point being made by the paper here is still true--that special forms are useful in controlling evaluation--is still true: SCHEME does use functions and closures a lot where Common Lisp uses special syntax, but SCHEME could use functions and closures more than it does, and chooses not to. IF itself does not need to be a piece of primitive SCHEME syntax--it's offered that way because it's syntactically convenient to do so. In other words, the key point being made here is not that special syntax is needed to do conditional evaluation, but that special syntax allows and is routinely used for this purpose.]
QUOTE'ing code will also confuse the compiler, since it will not realize that the objects are really to be used as program text rather than as quoted list structure. This will be discussed in more detail later.
It is also not adequate to use GENSYM's as variable names in our definition because GENSYM's are not visually distinguishable from interned atoms with the same printname. [This also later changed slightly in Common Lisp (1984) with the introduction of the ``#:'' syntax.] Hence, since Lisp's READ works by analyzing printed representation and creating interned symbols, such a definition would work in the environment in which it was created, but if saved via PRINT would not be functionally equivalent upon reloading since all the symbols which were originally GENSYM's would now be interned.
[At the time, especially in the INTERLISP and somewhat also in MACLISP, it was popular to spend a Lisp session typing expressions first to Lisp and only later printing and saving them. In more recent environments, it's more common to see code typed to a text editor and saved independently, so this role of PRINT has become deemphasized over time.]
We are clearly going to a lot of work to guarantee the semantics of our proposed IF definition. It will be shown in the next section that there is a simple and elegant way of dealing with this problem which avoids these issues of quoting, invalid evaluation contexts, and printed representation. Something more powerful is required or the user will have to resign himself to using COND or some other already-built-in special form for the rest of his life whenever he wants to express the notion of conditional evaluation or flow of control.
Special forms can also achieve a very powerful type of call by name functionality which affects the scope of variables. For example, MACLISP offers a very powerful primitive called SETF which acts as a sort of generalized SETQ. It allows the syntax
(SETF form value)
where if form is a symbol, it will be assigned as if SETQ had been used, but if form is not a symbol, an appropriate side-effect producing operation is selected to do the assignment. An illustration will make the functionality clearer:
(SETF (CAR form) value)(RPLACA form value) (SETF (CADR form) value)
As with some of our previous examples, it simply is not possible for a normal EXPR function to achieve the desired effect while retaining this simple syntax. Such expressiveness may be gained only through the use of special forms.
It may also be the case that there exists some function which is so often used in composition with itself, that we may wish to construct an n-ary version of that function which behaves as if it were a composition of the more primitive operator. The earliest Lisps did not have facilities for defining functions of a variable number of arguments, so the need was more critical then than now. However, for some applications, it may still be desirable in a modern Lisp dialect to implement functions such as these as special forms.
MACLISP and LISPMACHINE Lisp offer an operator named LIST* which may be thought of conceptually as being like a CONS function but allowing a variable number of arguments. In a Lisp dialect which did not have a primitive LIST* function, one might consider implementing the operation via a special form [4]. e.g.,
(LIST* form)
In Lisp and other languages, there may be a desire to achieve a sense of modularity without sacrificing efficiency. A problem which results from always doing function calling is that one may desire for the sake of style to separate out an operation and give it a name. If the operation itself requires less code than the call to that function, inefficiency will result.
For example, one may wish to speak in abstract terms, referring to NODE-NAME and NODE-DATA rather than CAR and CDR for some application. For example, creating the definitions
(DEFUN NODE-NAME (X) (CAR X)) (DEFUN NODE-DATA (X) (CDR X))
and then substituting calls to these functions for calls to CAR and CDR as appropriate, would result in a great slowdown due to the indirection through a second function call. What we would like is some way of specifying simple functional equivalences without introducing a large amount of extra overhead in terms of stack space and wasted instructions at execution time.
It should be clear, then, that special forms are useful in a wide variety of circumstances. The expressiveness which they offer can add much to the clarity of an individual's coding style. We can now approach the issue of how the definition of a special form should be specified.
One solution would be for the semantics of special forms to be described in some other language (e.g., Midas [5]). Such a solution, however, does not facilitate user extension of the language. It requires that a user of Lisp also be a user of whatever language his Lisp is implemented in terms of. It also makes for difficulty in terms of compilation--an issue which will be discussed in more detail later--because the compiler must have a great deal of special-case code to deal with information about the compilation of each special form.
The obvious solution for a language such as Lisp, in which program and data enjoy the same representation, is that special forms should be specified in the language itself. Unfortunately, the precise manner in which the specification can be achieved is less obvious. Several competing schemes for expressing the functionality of special forms have been devised and implemented in the major Lisp dialects. This section will present a brief overview of the essential features of those schemes.
The syntax for specifying a FEXPR in MACLISP is:
(DEFUN name FEXPR (variable) . body)
Like a normal, EXPR-style DEFUN, this form associates with the variable name a LAMBDA expression which is constructed from information supplied by a bound variable list--in this case, the one-length list containing variable--and a body. The thing which makes FEXPR's special is that additional information is stored with the symbol indicating that when the name occurs as the operator in a form, no evaluation is to be done on any part of the CDR of that form. Instead, the entire CDR is to be bound to variable, and then body is to be executed according to the normal rules for evaluating the body of a LAMBDA expression. The value returned by the application of the FEXPR definition to the CDR of the form is the value which is returned by the FEXPR-form.
Using FEXPR's to define our DESCRIBE example from before, one might say
(DEFUN DESCRIBE FEXPR (TOPIC-INFO)
(PRINC (LOOKUP-DOCUMENTATION
(CAR TOPIC-INFO))))
and thereafter be able to invoke DESCRIBE with the syntax (DESCRIBE keyword)--no quoting needed.
[Note: The reference to keyword here was not related to Common Lisp keywords. MACLISP had no keywords in that sense, nor in fact did it even have packages. This reference to a keyword was just about avoiding the quote in (DESCRIBE 'SOMETHING).]
INTERLISP offers something similar to FEXPR's with its NLAMBDA facility. The essential notion here is that the functional description itself should have information associated with it saying whether or not the arguments to that function should be evaluated. LAMBDA combinations involve the evaluation of each element in the argument specification list prior to functional application, while NLAMBDA combinations do not. e.g.,
(SETQ A 1 B 2 C 3)
LISPMACHINE Lisp offers a slightly more generalized syntax for achieving this end via their ``"E'' mechanism, which allows a marker to be placed in the bound variable list of the function saying which of the actual parameters should not be evaluated before application of the definition.
MACRO's offer a way of defining a mapping between a special form and an evaluable form--a transformation, written in the normal primtiives of the language, between pieces of code. These may be either transformations between a macro form and a piece of evaluable structure or between one macro form and another macro form.
The Lisp interpreter handles MACRO forms much differently than it handles other types of forms [6]. When a form is encountered, the CAR of which is defined as a MACRO, the macro definition (itself a function of one argument) is called with an argument which is the entire, unevaluated macro form and the value returned by the macro definition is then evaluated to produce a value which will be returned as the value of the MACRO form.
MACRO's have the syntax
(DEFUN name MACRO (variable) . body)
A MACRO definition of our DESCRIBE special form might look like this:
(DEFUN DESCRIBE MACRO (X)
(LIST 'PRINC
(LIST 'LOOKUP-DOCUMENTATION
(LIST 'QUOTE (CADR X)))))
or, perhaps, like this:
(DEFUN DESCRIBE MACRO (FORM)
(SUBLIS (LIST (CONS 'X (CADR FORM)))
'(PRINC (LOOKUP-DOCUMENTATION 'X))))
Lest the reader feel that this syntax is overly clumsy, it should be noted that we are oversimplifying things here for the sake of clarity. MACLISP and LISPMACHINE Lisp, employing the MACRO technology ideas advocated in this paper, allow the following alternate syntax for DESCRIBE's definition as a macro:
(DEFUN DESCRIBE MACRO (X) `(PRINC (LOOKUP-DOCUMENTATION ',(CADR X))))
How the read macro characters backquote and comma in this example are defined is of tremendous importance, but is beyond the scope of this paper. The important fact is that it would be naive to condemn MACRO's as overly complicated for practical use on the basis of the difficulty involved in writing the long-form definition.
[Note also that by this time the more modern DEFMACRO syntax later adopted by Common Lisp (1984), involving a multi-variable argument list with ``&OPTIONAL'' and ``&REST'' and other lambda list keywords, was already available even at the time this paper was written. I knew and used that syntax at the time, but in consultation with others as I prepared the paper, it was decided that the new syntax was too complicated to present. As aesthetically painful as it is now to read the old-style MACRO definition syntax using a single form argument, it was really quite ordinary-looking at the time, and since many people hadn't seen macro definitions at all, I and my paper's reviewers wanted to keep the paper simple by demonstrating only the minimal technology needed to illustrate the point.]
In MACLISP, all operator definitions are of effectively the same type--LAMBDA expressions. The difference between them is where the definition is stored. For example,
(DEFUN name bvl . body)
What is interesting here is not the names of the properties in which the expressions are stored--nor even the fact that the information is stored on the property list at all. The important thing is that all definitions are simple LAMBDA expressions. What has been done is to associate information with the symbol, name, describing any special treatment that is to be given its form before and after the application of the definition--but the function which is applied is just a garden variety function with no special information information attached to it.
Suppose, for example, that there exists some FEXPR named FEX which performs some useful function but which, because it is a FEXPR, is very cumbersome to use--requiring that APPLY always be used to call it in order to force the effect of argument evaluation. In MACLISP, because of the general nature of functional descriptions, it would be possible to borrow FEX's definition for a normal function, EX, by saying
(PUTPROP 'EX (GET 'FEX 'FEXPR) 'EXPR)
Having done so, the following equivalences would be true:
(FEX X Y Z)
In other words, the definition does exactly one thing. It describes what to do with a set of formal parameters. It puts no restrictions on the process of how those formal parameters are to become associated with their values [7]. Such a decision is left to the evaluator. We shall see another very useful example of this in a later section when we look in more detail at MACRO's and macro expansion.
In INTERLISP and LISPMACHINE Lisp, which allow the use of NLAMBDA style constructs, this is not the case. Function descriptions attempt to enforce a specific type of evaluation of actual parameters. In such a case, functional information is tightly coupled with evaluation information and more difficult to separate. It is the opinion of the author that performing this association is highly inappropriate and should be avoided. LAMBDA definitions should remain trivially separable from argument evaluation information. This separation provides not only for a more elegant theory, but is also more useful in practice, since in most practical cases evaluation and functionality are most usefully varied independently of each other.
One advantage of FEXPR's is that they are applicable [8].
(APPLY f form)
where f is a FEXPR, is defined to look up the
definition of f and bind to its single
-variable, the
object which is the result of evaluating form.
Hence, if DESCRIBE had been defined to be a FEXPR and
we later realized that we wanted to hand it the value of some variable
rather than a constant token, we could still get the desired functionality
by saying
(APPLY 'DESCRIBE (LIST TOPIC))
Another advantage of FEXPR's is that they are easily supported by a Lisp TRACE facility. Using TRACE with our DESCRIBE operator might produce the following [9]:
(TRACE DESCRIBE)
Debuggers that single-step the operation of FEXPR's are similarly trivial to write.
Perhaps the most important reason why MACRO's are important is that they offer transparency of functionality. It is possible, without evaluating the macro form, to determine what the form will do in terms of primitive Lisp operations. This is true because the macro definition need not be invoked only by the evaluator.
An interesting problem that one might face in writing programs that treat other programs as pieces of data is the desire to substitute some expression, new, for all evaluable occurrences of some other expression, old, in some third expression, form. It is not sufficient to use SUBST bevcause it may be that form contains some occurrences of old in positions which are not evaluable and for certain applications one would not want the substitution routine to enter forms which were not to be evaluated. For example,
(SUBST 'B 'A '(LAMBDA (A) (LIST 'A A)))
If the desired outcome had been
(LAMBDA (B) (LIST 'A B))
then SUBST would be inadequate.
One could imagine, therefore, writing a program, SMART-SUBST which knew about all the primitive special forms in Lisp and how to deal with them. Such a function could be made not to recurse inward upon encounter of a QUOTE-form. But a problem arises if a user-defined special form is encountered. We would certainly want our program to understand and deal correctly with special forms and their particular semantics. Now suppose we try our SMART-SUBST on an expression which involves a user-defined IF special form, as in
(SMART-SUBST 'B 'A '(LAMBDA (A) (IF A 'YES 'NO)))
A major drawback to the use of FEXPR's is that there is no reliable mechanism for determining which, if any, of the objects in the argument position will in fact be evaluated at some point in the future. Our SMART-SUBST program would have to infer here that A was not to be evaluated and the return value would be
(LAMBDA (B) (IF A 'YES 'NO))
If on the other hand, we used the MACRO definition
(DEFUN IF MACRO (X)
(LIST 'COND
(LIST (CADR X) (CADDR X))
(LIST 'T (CADDDR X)))),
we could define the following useful helping function
(DEFUN MACROEXPAND (X)
(LET ((MACRO-DEFINITION (GET (CAR X) 'MACRO)))
(COND (MACRO-DEFINITION
(FUNCALL MACRO-DEFINITION X))
(T X))))
and pass the IF-form to MACROEXPAND. The return value would be a COND-form, which SMART-SUBST would presumably know how to deal with since COND is a primitive special form.
(SMART-SUBST 'B 'A
'(LAMBDA (A) (IF A 'YES 'NO)))
[The original paper doesn't say, but the return value intended is presumably:
]
An interesting feature of MACRO's is their ability to run efficiently in the interpreter. Consider the definitions:
(DEFUN FIRST MACRO (X) (CONS 'CAR (CDR X))) (DEFUN PRINT-FIRST (X) (PRINT (FIRST X)))
Each time a call to (PRINT-FIRST expression) is executed, the computation of a transformation between (FIRST X) and (CAR X) would have to be recomputed. For the case of interpreted code, one might as well have defined FIRST by just
(DEFUN FIRST (X) (CAR X))
However, a trivial alteration to our macro definition will cause a large speedup in time:
(DEFUN FIRST MACRO (X) (RPLACA X 'CAR) X)
Note how upon the first call to PRINT-FIRST, the form (FIRST X) will be side-effected upon so that it is now just (CAR X). This means a later call to PRINT-FIRST will not invoke the macro at all, since the definition of PRINT-FIRST has been altered in a way that destroys any reference to the original call. Note that this sort of destructive effect may not be desirable if the code is being debugged, but it is available in a flexible way--the user has the option of selecting it or not, as he desires [10].
MACRO's have the unfortunate feature of being harder to trace with conventional Lisp TRACE and single-stepping packages. The reason for this is that what gets traced is the expansion, not the execution of the expansion. For example, if we trace our macro definition of DESCRIBE from the previous section, we observe the following:
(TRACE DESCRIBE)
This may or may not have been the desired result. In some cases it is useful to see the expansion traced, while in others it is more useful to see a trace of the functionality of the form (i.e., the sort of thing we observed on entry to the DESCRIBE FEXPR earlier).
The question of whether to use FEXPR's or MACRO's to solve a particular problem may seem purely an issue of style. However, with the introduction of the concept of compilation, it becomes much more clear that FEXPR's and NLAMBDA's are not only inadequate for handling all of these cases correctly, but actually make it impossible for MACRO's to do their job correctly in the general case.
Compilation involves taking Lisp code and producing a sequence of machine instructions which when executed will behave in a manner which is functionally equivalent to that of the source program. Compilation is perhaps more well-defined in languages which do not support Lisp's powerful ``Program is Data--Data is Program'' feature. In particular, it is not necessarily obvious what pieces of a program may be ``compiled away'' and which must be retained in the interpreter-style format of list structure in order to function correctly.
[In modern Lisps, such as Common Lisp, this issue no longer arises. Though never explicitly spoken about this way, I think the major shift is that when documentation and implementation did not agree in older Lisp dialects, the documentation was usually defined to be wrong and in need of repair. Once in a while, the implementation didn't deliver what was promised, but more often than not, it was the other way around.
In modern Lisps, when a dispute arises between documentation and implementation, the documentation is generally defined to be correct from the outset, and so it's the implementation that needs to be repaired if a discrepancy between documentation and implementation arises.]
The job of the compiler [11] is to try to reduce Lisp code into a set of machine instructions which have equivalent functionality. This may be harder than it sounds because to do this correctly may require answers to questions which are not answerable by the compiler.
Consider the following sets of definitions:
(DEFUN F1 (X) (G1 X)) (DEFUN G1 (X) (+ X Y)) (DEFUN F2 (X) (G2 X)) (DEFUN G2 (Y) (+ Y X))
In the case of F1, there would be no loss of functionality
for the compiler to compile F1 as simply a jump to G1,
without bothering to do any further binding. It should be obvious,
however, that the compiler could not get away with just a jump to
G2 from F2, despite the fact that their syntactic structure
is nearly identical. This is called the problem of special variables
and is related to the issue of dynamic scoping which was addressed earlier.
Some -variables
are created just because it is necessary to have a name
to refer to a local variable while others are created for the purpose of
communication between a given function and other functions which that
function calls. Variables of the latter kind are called SPECIAL
and must be declared so in the MACLISP compiler in order to generate
correct code.
[Note that in MACLISP there was not, as occurred in later dialects, a language definition organized around the idea that ``interpreted semantics'' and ``compiled semantics'' should be indistinguishable. As a result, it was commonplace for certain code to ``only work in the compiler''. This misfeature of early Lisps is not present in more modern Lisps, such as Common Lisp, which have a semantics that is more uniform between interpreter and compiler.
Note further that MACLISP was defaultly dynamically scoped in the interpreter, but was lexically scoped when compiled unless a SPECIAL declaration was used to assure that the ``specialness'' of a variable was preserved in compiled code.]
The special variable problem is a good illustration of a whole class of issues with which the compiler must deal in order to generate efficient code. The Lisp compiler is constantly making decisions about what kind of machine code would be an appropriate representation for a given specification in normal Lisp notation. Appropriate use of special forms may be able to greatly enhance the decision process as we shall see in this section.
In the compiler, MACRO's are used to transform source code into compilable code which contains no MACRO forms. Hence, a MACRO definition can in some sense afford to use more time in its transformation than any other type of operator can afford to do in similar case analysis at runtime. This is because a macro form will be expanded exactly once (at compile time) while any other type of operator may be called repeatedly at runtime and will have to make decisions anew each time it is called.
Since MACRO's run in the compiler, there is no runtime overhead in indirecting through their definition. Additionally, because the code into which a macro expands is placed inline at the point of the macro call, rather than separated off by itself as occurs with functions, the compiler may be able to do very efficient coding for any given usage of the macro. If the operator had been an applicable operator (EXPR or FEXPR, for example), rather than a macro, the compiler might have to sacrifice efficiency for generality, since it would not know what the actual intended use of the function was to be, and a less efficient compilation might result.
We should also keep in mind that functions have to be jumped to, macros do not. Very small functions may well spend more time in being called than in performing the action for which they were called. Function calling may involve shuffling accumulators into some standard configuration or saving/restoring accumulators that may be clobbered in the call. Rewriting short, frequently-called functions as macros may well provide an increase in speed for this reason.
It has been argued that FEXPR's are necessary to implement certain special forms because if the amount of code involved is large, a FEXPR-style solution is apt to be more space-efficient than one which employs MACRO's. The reason for supposing this to be true is that every call to a MACRO will expand into that large piece of code.
It is certainly possible to construct a MACRO definition which is wasteful in this way, but if space limitation problems do arise, there is a standard formula for producing a macro which provides essentially the same functionality as any given FEXPR.
(DEFUN f FEXPR (var) . body)
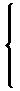
(DEFUN f MACRO (FORM) (LIST 'EXPR-f (LIST 'QUOTE (CDR FORM)))) (DEFUN EXPR-f (var) . body)
Having done this transformation, however, one will no longer be able to use the operator APPLY on f. But since the primary use of APPLY is to force evaluation of the FEXPR arguments which would formerly not have evaluated, it would seem reasonable to replace any calls to APPLY with direct references to the function EXPR-f.
(APPLY 'f expression)
In other words, changing from FEXPR's to MACRO's cannot be done by merely changing the definition; some changes to source code may be necessary where operators like FUNCALL and APPLY have been used. But no major restructuring of the code is necessary.
MACRO's are also powerful enough to provide extended scoping rules that other types of function definitions cannot. They can, for example, define a piece of code in terms of a variable which is local to another operator without the use of special variables. Consider the following variation on our F1/G1-F2/G2 examples from before:
(DEFUN G3 MACRO (FORM)
(LIST '+ (CADR FORM) 'X))
(DEFUN F3 (X) (G3 X))
Upon MACRO expansion, the F3 definition will become
(DEFUN F3 (X) (+ X X))
Another example of this type of scoping power involves PROG and RETURN. Suppose we found it desirable to have a special form named TRY, which when executed would evaluate the objects in its CDR sequentially, allowing early return by means of operators FAIL and SUCCEED. As it happens, definitions of the form
(DEFUN FAIL (WHY?)
(RETURN (CONS 'FAIL WHY?)))
(DEFUN SUCCEED (HOW?)
(RETURN (CONS 'SUCCEED HOW?)))
(DEFUN MAIN ()
(PROG () ... (FAIL 'ERROR)
... (SUCCEED expression)))
would succeed in the interpreter, but could not be compiled. The compiler will turn GO's and RETURN's into a single jump instruction which jumps to the appropriate tag or to the return point of a PROG. If an isolated program, such as FAIL or SUCCEED, does a RETURN while not inside a PROG, no such jump instruction can be created since there is no way of knowing where to jump to until runtime. Hence, compilation of this code will fail.
[In the interpreter, MACLISP implemented GO and RETURN as if by a THROW to an internal tag in the innermost dynamically enclosing PROG so that the implementation accidentally permitted GO and RETURN to work even through a function call in interpreted code. This didn't ``work'' in compiled code.]
However, a MACRO definition of this form will succeed. The forms
(DEFUN FAIL MACRO (FORM)
(LIST 'RETURN
(LIST 'CONS ''FAIL (CADR FORM))))
(DEFUN SUCCEED MACRO (FORM)
(LIST 'RETURN
(LIST 'CONS ''SUCCEED (CADR FORM))))
would be macroexpanded by the compiler in the definition of MAIN and the code resulting from the transformation would be within the scope of the PROG.
Both FEXPR's and MACRO's suffer from the need for declaration in the compiler. In the case of a FEXPR, f, the declaration simply states that upon any references to f, the compiler is not to generate code for evaluating the elements in the CDR of f's form. While MACRO's require no explicit declaration, their definition must occur prior to reference to them in a file, since the compiler will attempt to expand any macro as soon as it is encountered.
Perhaps it is also a flaw in the specifications for FEXPR's that no declarations are required in the interpreter. This makes dealing with FEXPR's in the interpreter exceedingly tricky because programmers are taught that the definition need not be available until the function is actually called. The nature of MACRO's, on the other hand, effectively constrains them to be defined in the environment earlier than the time at which they are actually called.
It should be clear from this discussion that FEXPR's are only safe if no part of their ``argument list'' is to be evaluated, and even then only when there is a declaration available in the environment in which they appear. Using FEXPR's to define control primitives will be prone to failure due to problems of evaluation context and due to their potential for confusing program-manipulating programs such as compilers and macro packages.
MACRO's on the other hand, offer a more straightforward and reliable approach to all of the things which we have said should be required of a mechanism for defining special forms. They can handle problems from implicit quoting to definition of control structure in a very straightforward way because they are functionally transparent; macro forms whose meaning is not understood may be expanded to produce forms whose meaning can be understood.
It is widely held among members of the MIT Lisp community that FEXPR, NLAMBDA, and related concepts could be omitted from the Lisp language with no loss of generality and little loss of expressive power, and that doing so would make a general improvement in the quality and reliability of program-manipulating programs.
There are those who advocate the use of FEXPR's, in the interpreter for implementing control structure because they interface better with certain kinds of debugging packages such as TRACE and single-stepping packages. Many of these people, however, will admit that calls to FEXPR's used as control structure are bound to confuse compilers and macro packages, and that it is probably a good idea, given that FEXPR's do exist, to require compatible MACRO definitions be provided by the user in any environment in which FEXPR's will be used. This would mean that a person could create a FEXPR named IF, provided he also created an IF MACRO which described its behavior; the FEXPR definition could shadow [12] the MACRO definition in the interpreter, but programs other than the interpreter could appeal to the MACRO definition for a description of the FEXPR's functionality.
The NIL dialect will not support FEXPR's, NLAMBDA's or "E-like constructs at all. The intent there is that there should be a minimal number of operators like QUOTE and COND which must really be treated specially. All other primitives are not of this type. This means that program-manipulating code can be written which special-cases these basic primitives without fear that such code will later break due to the implementation of other such forms by the user. The functional transparency provided by MACRO's makes new control primitives automatically compatible with pre-existing code-manipulating packages.
It would seem that NIL has taken the right step. It would be naive to expect that FEXPR's and NLAMBDA's will ever be flushed from existing dialects. In spite of their problems, much useful code has been written to depend on them and the job of changing all of this code would be tremendous. In looking toward the future, however, serious thought should be given to whether or not such constructs really have a place in the language. If it is determined that they do have a place, greater consideration should be given to the declarations, particularly the requirement of compatible macro definitions, in order that other software may achieve higher reliability in an environment in which FEXPR's and NLAMBDA's exist.
John R. Allen: Anatomy of Lisp, McGraw-Hill, Inc., 1978.
Charniak, Riesbeck, and McDermott: Artificial Intelligence Programming, Lawrence Erlbaum Associates, Hillsdale, NJ, 1980.
Bernard Greenberg: Notes on the Programming Language Lisp, Student Information Processing Board, MIT, 1978.
John McCarthy: Lisp 1.5 Programmer's Manual, MIT Press, Cambridge, MA, August, 1962.
David A. Moon: Maclisp Reference Manual, Laboratory for Computer Science, MIT, March 1974.
Guy L. Steele, Jr.: Rabbit: A Compiler for Scheme, AI-TR-474, Artificial Intelligence Laboratory, MIT, May, 1978.
Guy L. Steele, Jr. and Gerald J. Sussman: The Revised Report on SCHEME, A Dialect of Lisp, AI Memo 452, Artificial Intelligence Laboratory, MIT, January 1978.
Warren Teitelman: Interlisp Reference Manual, Xerox Palo Alto Research Center, October 1978.
Daniel Weinreb and David Moon: Lisp Machine Manual, Artificial Intelligence Laboratory, MIT, January 1979.
Jon L. White: ``NIL--A Perspective'', 1979 Macsyma Users' Conference Proceedings; Washington, DC; June 20-22, 1979.
Patrick Winston and Berthold K. P. Horn: LISP, Addison Wesley, 1980.
I would like to extend my thanks to Jonathan Rees, Robert Kerns, Ed Barton, Guy Steele, Alan Bawden, Bill Dubuque, Robert Handsaker, Richard Bryan, Jonl White, Barry Trager, and Jim O'Dell for their very useful comments and criticisms on developing drafts of this paper.
[Footnotes]
(PUTPROP 'QUOTE (GET 'CAR 'SUBR) 'FSUBR)for a striking illustration of this phenomenon. Except for a slight reduction in error checking, the Lisp should continue to function correctly despite the seemingly drastic nature of this incantation.
Original printed text document
Copyright 1980, Kent M. Pitman. All Rights Reserved.
HTML hypertext version of document
Copyright 1998, Kent M. Pitman. All rights reserved.
The following limited, non-exclusive,
revokable licenses are granted:
Browsing of this document (that is, transmission and display of a temporary copy of this document for the ordinary purpose of direct viewing by a human being in the usual manner that hypertext browsers permit such viewing) is expressly permitted, provided that no recopying, redistribution, redisplay, or retransmission is made of any such copy.
Bookmarking of this document (that is, recording only the document's title and Uniform Resource Locator, or URL, but not its content, for the purpose of remembering an association between the document's title and the URL, and/or for the purpose of making a subsequent request for a fresh copy of the content named by that URL) is also expressly permitted.
All other uses require negotiated permission.